02 May Aberration Correction in Computer-Generated Holography
Aberration correction was the topic of a mini-project I completed as a part of the MRes programme at the Centre for Doctoral Training in Connected Photonics and Electronics between Cambridge and UCL.
It ended up being a topic so deep and exciting that I spent most of my PhD brain power exploring the depths of it. I published several papers on the topic, including the 2016 Optics Express publication “Adaptive, spatially-varying aberration correction for real-time holographic projectors”.
In the paper, a variety of corrections was presented which can be incorporated into holographic projectors. A very handy feature of those correction methods is that they work on any projector and do not require any modifications to the setup. Put simply, a holographic projector which has been fully assembled, can simply be examined, characterised, and corrected, leading to diffraction-limited image despite its imperfect optics.
In addition, real-time generation of holograms, which incorporate all the corrections, was shown. I demonstrated the real-time operation on a YouTube stream of Dire Straits (choice of music was a bit of a personal touch; I did see Mark Knopfler live, and it was as amazing as you can imagine!).
This post summarises the findings, and goes a little beyond including some elements I learnt long after.
Aberrations are phase errors of the wavefront
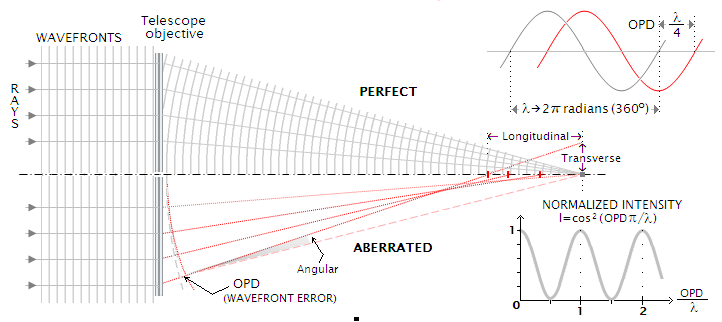
The handy property of optical aberrations is the fact that they reside solely in the phase of the wavefront without affecting its amplitude. That has been a great insight of Frits Zernike, Nobel Laureate and inventor of the Phase Contrast Microscope.
Indeed, that makes intuitive sense if one keeps in mind the correspondence between wave and geometric optics. Wavefronts are perpendicular to the rays of light (as pictured below). And so the parabolic wavefronts neatly focus onto a single spot. If the wavefront contains some error, rays will deviate from their perfect direction leading to the overall blurry image.
Zernike Polynomials neatly describe different aberrations
Zernike Polynomials are useful in many ways. The most important is the fact that they correspond to known optical aberrations.
Mathematically, they form a complete infinite set over the unit circle, meaning that, in principle, any function can be represented exactly (given an infinite number of terms). Even if that number is finite, most smooth functions can be well approximated.

Throughout my life, I’ve worked with a maximum of 13 terms (z3 – focus to z15 – primary spherical; using University of Arizona/Wyant Numbering Scheme). Even with as little as 13 terms, I was capable of achieving a satisfactory correction on all projectors I’ve dealt with.
Holography and aberration correction
A match made in heaven
Holography, unlike any other display technology I know of, retains and uses the phase information of the beam. Phase-only holograms (or Kinoforms as they’re sometimes called), are fully transparent and use solely the phase of the beam to form holographic replays.
It is then straight-forward to see how Aberration correction and CGH is a match made in heaven. It costs little overhead to apply the aberration correction to CGH, and the process is exceedingly simple. One calculates the phase mask by a weighted sum of Zernike Polynomials:
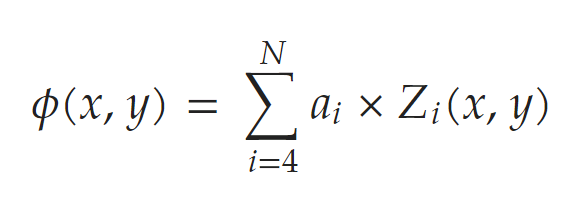
…. and uses that as an offset to the hologram’s phase:
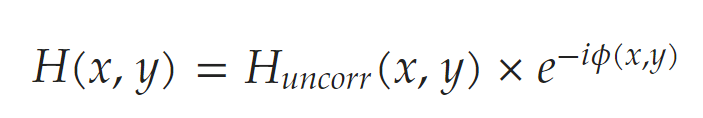
It really is that simple!
Conceptually, we’re introducing “artificial aberration” into the beam, which then cancels the aberration of our optical system (as seen in the figure below).
Field-Dependent Aberrations
Actually, described above is the recipe for correcting field-independent (or field-invariant) aberrations – errors which are constant across the entire image. Correcting field-dependent aberration is also possible, and this is actually the main focus of the 2016 paper.
Conceptually, this is achieved in a few steps. First, assume that the aberrations vary slowly throughout the image. Then divide the replay field into “pieces”, which are meant to be small enough so that the aberrations within the pieces are approximately constant. Following this thought process, field-dependent aberrations are replaced by a number of easy to correct field-independent problems for a number of sections of the image.
If we know those aberrations precisely (either by computation or experiment), we can construct the hologram which corrects them.
It doesn’t come without trade-offs however. The price we pay is that the more “regions” we’d like to have, it extends the computation time. For now the computation is a bottleneck, but it won’t be for much longer. In 2015, the code I wrote reached 12 frames per second on a very modest GPU (check out the video below as a proof):
In Summary
1. Aberration correction is a neat feature of holography, which is not possible in other display types
I used to joke that I specialised in holographic aberration correction because aligning optics was not my strongest suit 🙂
Despite my fairly modest (at the time of my PhD) optics design and alignment skills, I was routinely achieving diffraction-limited performance from the optical systems I built.
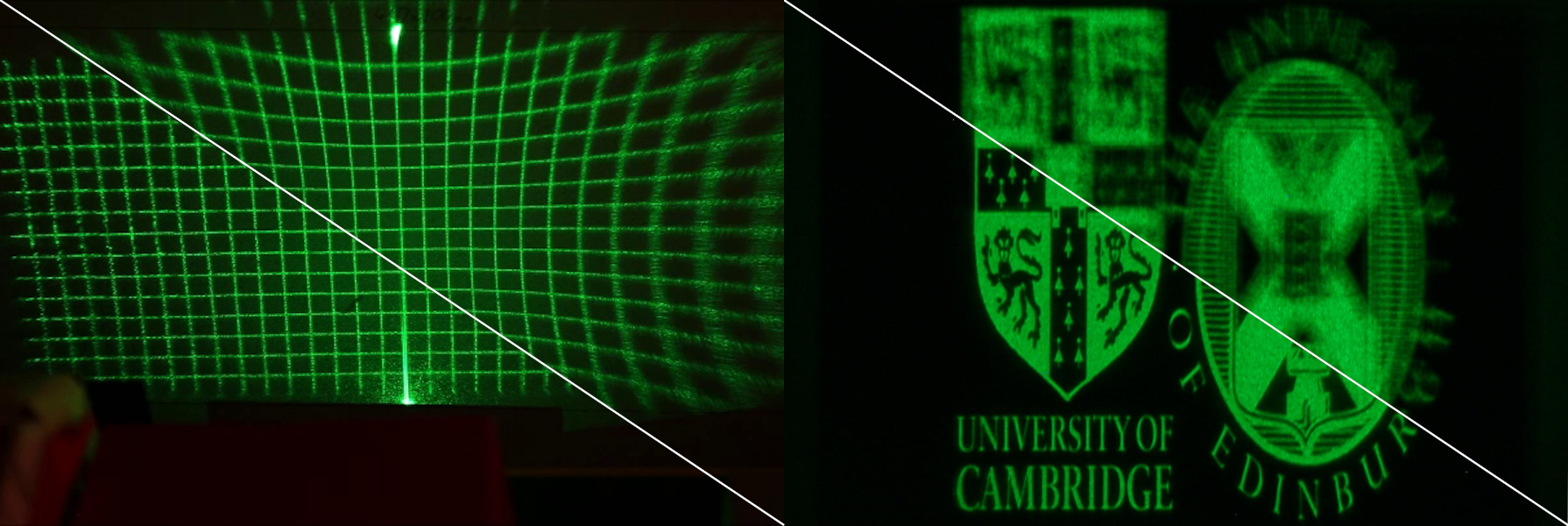
The correction I’m most proud of was done on the projector I built in collaboration with Dr Philip Hands from Edinburgh University. The single point before-after the correction can be seen below:
and the corresponding test image:

Field-independent aberrations are trivial to correct with very little computational overhead. That also generalizes to chromatic aberrations. Field-dependent aberrations are a bit more challenging. In order to correct them, one should be prepared to pay with additional computation.
2. Aberration correction makes optical design easier
Imagine designing the optical engine of AR Smart Glasses. Getting a supreme performance over the entire image is a challenging task. Usually, the degrees of freedom available to optical engineers are: surface curvature profile, thickness, position and choice of glass.
Aberration correction makes achieving supreme performance (and to a large extent the size of those devices) a much simpler problem to have.
Optical designers can simply compromise on some properties of the system by having assurance that some leftover errors can be corrected after the fact.
3. New developments since 2015/2016
Since writing the paper, I learnt some of the most surprising ways in which aberration correction comes in handy:
Phase Errors of the Light Source
Laser diodes are often astigmatic with an elliptical beam profile. Alongside the amplitude variation, we also see a strong phase variation across the beam. Long story short – holographic projectors illuminated by small and inexpensive laser diodes, would naturally exhibit astigmatism. Luckily for us, this can be corrected with a single phase mask.
Fine Control of the beam direction and focus
Certain optical systems rely on very precise collimation of the beam. For instance, when coupling your image into the waveguide, the efficiency and the performance of the process will depend on how close we’re to optical infinity. Even small changes get magnified with every pupil replication. And if we’re dealing with 10s or 100s reflections before we reach the eye, well … you get an idea. Holography gives us that flexibility for free. Focus is merely the third Zernike polynomial (or parabolic phase factor), the computational overhead of applying this to your beam is negligible.
Chromatic Aberration Correction is far more useful than anticipated
Chromatic Aberrations are hardly new. The established solution to eliminate them is by using achromatic doublet lenses.
Additionally, holographic projectors very often achieve colour by sequencing laser pulses in colour-field sequential fashion. This practically means that colours are naturally “decoupled” from one another. Which in turn means that chromatic aberration is merely a field-independent aberration from the correction point of view.
Now, this is hardly anything new. Truth is, I underestimated the usefulness of it. As it turns out, the ability to use singlet lenses instead of achromatic doublets makes the life of optical designers much easier.
3D Hologram can be described as an aberration
One can think about 3D directly-viewed holograms as being composed of layers which are then focused at different distances. As it happens, the mathematical representation of this problem and the one of correcting field-dependent defocus aberration is equivalent. The same base algorithm that allowed us to achieve 12 frames per second hologram generation at the time of writing the paper, ran the Holo-over-IP demo a year later. This requires a little more explanation, and will be the topic of a future post – coming soon!
Further Reading and References
Adaptive Aberration Correction for Holographic Projectors
“Adaptive, spatially-varying aberration correction for real-time holographic projectors”.

